光デバイス/光制御素子
8.電気光学効果
前項で屈折率変化を利用した光変調について概観し、この種の光変調は多岐に及んでいることを示しました。この項以降、これらのうち、主なものについて説明していきます。まず前項(2)屈折率を変化させる手段について順に紹介していきます。
誘電体の屈折率を制御するためには何らかの外力を加える必要があります。この外力は力学的な力であってもよく、また電界や磁界等を用いることもできます。これらの外力の効果による屈折率の変化を理論的に扱う方法はほぼ共通しています。しかしあまり一般的な説明をするとわかりにくくなってしまうので、まずは電界による効果について説明します。
結晶中を進む光の性質については「結晶光学」11項で説明したように屈折率楕円体を用いて端的に表すことができます。その楕円体の方程式は次式で表されます。
\[\frac{x^2}{n_x^2}+\frac{y^2}{n_y^2}+\frac{z^2}{n_z^2}=1\tag{1}\]
この式が表す回転楕円体は主軸がx,y,z方向であり、その長さは \(n_x\)、\(n_y\)、\(n_z\) になっています。この楕円体を光の進行方向に垂直な面で切断し、その断面の楕円の方程式を求めます。この楕円の長軸および短軸の方向がこの結晶内での2つの偏光方向となります。またこの2軸の長さの1/2がそれぞれ2つの屈折率の値となります。したがってこの結晶内で光は真空中の光速をこの2つの屈折率で割った2つの位相速度で進行することになります。
さてここでこの結晶に電界を加えたとき、どのような変化が起こるかを考えます。もちろん結晶に進入する光は電磁波ですから、振動する電界が結晶を構成する原子と相互作用をします。ここで言う結晶に加える電界は光の振動数に比べて十分遅い振動数の電界、通常は一定の電界です。原子は光の電界によって分極が変化しますが、これとは別に一定の電界による分極が重畳することになります。
この一定電界による分極は誘電率に何らかの影響を及ぼすはずですが、その影響は結晶構造に依存し、正確に記述するのは困難です。ただその影響は(1)式の回転楕円体を変形させるはずです。その変形した楕円体の方程式を一般的に書くと次式のようになるとしてよいと考えられます。
\[\left (\frac{1}{n^2}\right )_1 x^2+\left (\frac{1}{n^2}\right )_2 y^2+\left (\frac{1}{n^2}\right )_3 z^2+2\left (\frac{1}{n^2}\right )_4 yz+2\left (\frac{1}{n^2}\right )_5 xz+2\left (\frac{1}{n^2}\right )_6 xy=1\tag{2}\]
(2)式は電界 \(E=0\) のとき、(1)式に一致しなければならないので
\[\begin{align}\left (\frac{1}{n^2}\right )_1\Bigg |_{E=0} &= \frac{x^2}{n_x^2},~~~~~~~~~~\left (\frac{1}{n^2}\right )_2\Bigg |_{E=0} =\frac{y^2}{n_y^2},~~~~~~~~~~\left (\frac{1}{n^2}\right )_3\Bigg |_{E=0} =\frac{z^2}{n_z^2} \\ \left (\frac{1}{n^2}\right )_4\Bigg |_{E=0} &= \left (\frac{1}{n^2}\right )_5\Bigg |_{E=0} =\left (\frac{1}{n^2}\right )_6\Bigg |_{E=0} =0\end{align}\]
が成り立ちます。
ここで考えているのは屈折率の電界による変化ですが、(2)式では、\( (1/n^2 )_i ~~~(i=1,\dots ,6)\) が係数になっていますから、この各係数の電界依存性を考えることになります。\(1/n^2 \) は比誘電率 \(\varepsilon_r \) の逆数に相当しますから、\(\varepsilon_r^{-1} \) の電界依存性を考えるのが慣例になっています。本来ならば一定電界がかかっている状態の結晶に光が入射した場合に、個々の原子がどのように分極するかを考えることになりますが、非常に複雑な話になります。そこでまずは 比誘電率の逆数 \(\varepsilon_r^{-1} \) が、印加された静電界 \(\boldsymbol{F}\) (光波の電界成分\(\boldsymbol{E}\) と区別します)の大きさに対して何らかの関数で依存すると考えます。そしてこの関数を \(\boldsymbol{F}\) で級数展開した関数で近似できるとします(1)。すなわち
\[\varepsilon_r^{-1}(\boldsymbol{F})=\varepsilon_r^{-1}(0)+[r]\boldsymbol{F}+[s]\boldsymbol{F}\cdot\boldsymbol{F}+\cdots\tag{3}\]
と書けるとします。\([r]\)、\([s]\) はそれぞれ1次、2次の展開係数で、3階および4階のテンソルとなります。上式をxyz座標成分に展開しますが、表記を簡単にするため、\(\varepsilon_{r,ij}^{-1}(F)\) を \(a_{ij} (F)\) と置き換えることにします。念のため、\(\boldsymbol{F}=0\) のときの電界 \(E_i\) と電束密度 \(D_j\) の関係を\(a_{ij}\) を用いて記しておくと
\[\pmatrix{E_x \cr E_y \cr E_z}=\frac{1}{\varepsilon_0}\pmatrix{a_{xx}(0) & a_{xy}(0) & a_{xz}(0) \cr a_{yx}(0) & a_{yy}(0) & a_{yz}(0) \cr a_{zx}(0) & a_{zy}(0) & a_{zz}(0)}\pmatrix{D_x \cr D_y \cr D_z}\]
となります。\(\varepsilon_0 \) は真空の誘電率です。(3)式を展開すると
\[a_{ij}(F_i)=a_{ij}(0)+r_{ijk}F_k +s_{ijkl}F_k F_l +\cdots\tag{4}\]
となります。
さて、電気光学効果とは物質に電界を印加すると屈折率が変化する現象を言いますが、(1)式の屈折率楕円体が電界印加によって(2)式の屈折率楕円体屈折率に変化したとき、屈折率の変化はどう表されるでしょうか。
(1)式と(2)式の楕円体の概略の様子を図示すると、図8-1のようになります。印加電界 \(F\) が 0 のとき、(1)式の楕円体は図の青線で示すような楕円体となります。このとき、xyz方向の屈折率は楕円体と座標の交点で示されます。すなわち、それぞれxyz方向のもっとも長い径の値となります。このときのxyz軸を主軸と呼びます。
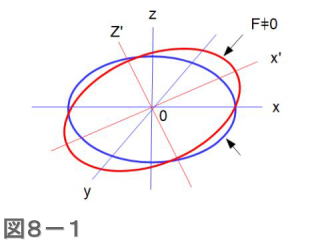
電界が印加された場合、楕円体は(2)式のように変化します。これは赤線で示すようなxyz軸に対して回転した楕円体になります。このとき、屈折率が変化しますが、変化した屈折率の値はxyz軸との交点からは求められません。回転したx’y’z’座標軸(図ではy’軸を省略しています)に楕円体の新しい主軸となりますから、これを求めなければなりません。この座標軸の変換を主軸変換といいます。
これを求めるのは解析幾何学の計算問題になります。やや脇道が長くなりますので「付録2」に記載することにします。以下もう少し具体的な説明をします。
(1)1次の電気光学効果(ポッケルス効果)
上式のようにある関数を級数展開した場合、通常は低次の項が支配的になります。つまり比例関係からそう大きくは外れません。そこでまず1次の項を考えます。1次の電気光学効果はポッケルス(Pockels)効果とも呼ばれています。この1次の効果は実は等方性の物質では現れません。いま結晶中の位置ベクトル \(\boldsymbol{r}\) を \(-\boldsymbol{r}\) に移す空間反転操作を考えます。操作後のベクトルを \(r'_{ijk}\) とすると、等方性の物質では空間反転操作によって性質は変わらず符号のみ反転しますから、\(r'_{ijk}=-r_{ijk}\) でなければならず、したがって \(r_{ijk}=-r_{ijk}\) が成り立つ必要があります。これが満たされるためには \(r_{ijk}=0\) でなければならず、等方性物質では1次の効果は現れないということになります。
以下では異方性結晶の代表的例として一軸性結晶(「結晶光学」12項参照)を取り上げます。一軸性結晶の屈折率楕円体は
\[\frac{x^2 +y^2}{n_o^2}+\frac{z^2}{n_e^2}=1\tag{5}\]
と表されます。これに電界を印加したとき、楕円体の変化は(2)式を参照して
\[\left(\frac{1}{n_o^2}+r_{1k}F_k \right)x^2 +\left(\frac{1}{n_o^2}+r_{2k}F_k \right)y^2 +\left(\frac{1}{n_e^2}+r_{2k}F_k \right)z^2 +2\left (r_{4k}yz+r_{5k}zx+r_{6k}xy \right )F_k =1\tag{6}\]
と書けると考えられます。(4)式右辺は第2項までとって
\[\begin{align}a_{ij}(F_k) &= a_{ij}(0)+r_{ijk}F_k \\ &= a_{ij}(0)+\sum\limits_{k=1}^3 r_{ijk}F_k \\ &= a_{ij}(0)+r_{ijx}F_x +r_{ijy}F_y +r_{ijz}F_z\tag{7}\end{align}\]
となります。「結晶光学」8項で示している通り、誘電率テンソルは対称です。したがって逆誘電率テンソルも対称で、\(a_{ij}=a_{ji}\) です。このため
\[a_{ij}(0)+r_{ijk}F_k =a_{ji}(0)+r_{jik}F_k\]
が成り立ち、\(F_k =0\) の場合は \(a_{ij}(0)=a_{ji}(0)\) ですから
\[\sum\limits_{k=1}^3 r_{ijk}F_k =\sum\limits_{k=1}^3 r_{jik}F_k\]
が任意の \(F_k\) について成り立つ必要があり、したがって
\[r_{ijk}=r_{jik}\]
が成り立ちます。本来3階のテンソル \(r_{ijk}\) は \(3\times 3\times 3=27\) 個の要素を持ちますが、上記の条件から独立な要素は \(3\times 3\times 2=18\) 個に減少することになります。印加電界 \(F_k\) は3次元方向の成分をもちますから、\(k\) は1,2,3 です。一方、逆誘電率の方はxx,yy,zz,yz,zx,xy の6元で、\(i=1,2,3,4,5,6\) となります。この6行3列のテンソル \(r_{ik}\) を電気光学定数テンソル、あるいはポッケルス係数と呼びます。\(\Delta a_{i}=a_{i}(F_k)-a_{i}(0)\) と置いて、\(r_{ik}\) を要素に展開して書くと
\[\pmatrix{\Delta a_{1} \cr \Delta a_{2} \cr \Delta a_{3} \cr \Delta a_{4} \cr \Delta a_{5} \cr \Delta a_{6}}=\pmatrix{r_{11} & r_{12} & r_{13} \cr r_{21} & r_{22} & r_{23} \cr r_{31} & r_{32} & r_{33} \cr r_{41} & r_{42} & r_{43} \cr r_{51} & r_{52} & r_{53} \cr r_{61} & r_{62} & r_{63}}\pmatrix{F_1 \cr F_2 \cr F_3}\tag{8}\]
となります。この電気光学定数テンソル \(r_{ik}\) の特徴、どの要素が 0 か、0 でない要素の値、が結晶構造と対応します。
以下、二、三の具体的材料を挙げて説明します。
例1.閃亜鉛鉱型結晶
この「小さな石たちの物語」はもともと半導体デバイスについて紹介するのを目的としていますが、半導体結晶にも電気光学効果をもつものがあります。光デバイスに用いられる代表的な半導体であるGaAsやInPなどはいずれも閃亜鉛鉱型あるいはジンクブレンド(Zincblend)型と呼ばれる結晶系をもっています(「結晶の話」10項参照)。この結晶型は(\(\overline43m\))と書かれる立方晶で対称性が高く、上記の一軸性結晶ではありませんが、比較的わかりやすい例と言えるので、ここではまずこの例を用いて \(r_{ij}\) の要素の決定の仕方を説明します。
まず、(5)式を(6)式に代入すると
\[\left\lbrace r_{1k}x^2 +r_{2k}y^2 +r_{3k}z^2 +2\left (r_{4k}yz +r_{5k}zx +r_{6k}xy \right )\right\rbrace F_k =0\tag{9}\]
となります。この式は(5)式で表される楕円体と(6)式で表される楕円体の表面が交わる曲線を表しますから、結晶に対称操作を施しても変化しません。
\(\overline43m\) 結晶は立方晶で、4回回転軸をもちます。図8-2に示すように立方体の稜に沿ってxyz軸をとると、xyzの各軸のまわりの180°回転に対して変化がないことが必要です。x,y,z方向の電界成分を \(F_1\)、\(F_2\)、\(F_3\) とし、各座標軸の周りに180°回転したときの座標と電界成分の変化を見ます。
いま図のようにx軸の周りに180°の回転を行ったとすると、x座標、\(F_1\) は不変ですが、y座標、z座標は反転するので、\(F_2\)、\(F_3\) はともに \(-F_2\)、\(-F_3\) となります。この回転によって物質によって決まる定数である \(r_{ij}\) は変化しません。したがって(9)式の各項がこの回転によって符号を変えるかどうかをみて、符号が変わる項の \(r_{ij}\) は 0 でなければならないことがわかります。結論としては \(r_{12},r_{13},r_{23},r_{32},r_{33},r_{42},r_{43},r_{51},r_{61}\) はすべて 0 となります。
つぎにy軸の周りに180°回転した場合から、\(r_{11},r_{21},r_{31},r_{53},r_{63}\) も 0 であることがわかります。
さらにz軸周りに90°回転した場合、\(x \rightarrow y\) となるので、\(F_1 \rightarrow F_2 \) となり、\(y \rightarrow -x\) となるので、\(F_2 \rightarrow -F_1\) と変換されます。zは不変です。これより \(r_{41},r_{52},r_{63}\) だけが 0 でないことがわかります。
\(\overline43m\) 結晶ではさらに図8-3に示すように立方体の対角線の周りに3回回転軸があります(「結晶の話、10項参照)。対角線周りに120°回転しても変化がないことになります。いまこの3回回転軸方向に電界 \(F\) をかけると \(F_1=F_2 =F_3 =F/\sqrt{3}\) ですから、 \(r_{41}=r_{52}=r_{63}\) であることがわかります。
以上より \(\overline43m\) の電気光学定数テンソルは
\[\pmatrix{0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr r_{41} & 0 & 0 \cr 0 & r_{41} & 0 \cr 0 & 0 & r_{41}}\]
となります。したがって
\[\begin{align}\Delta a_{1} &= \Delta a_{2}=\Delta a_{3}=0 \\ \Delta a_{4} &= r_{41}F_1 ,~~~~~\Delta a_{5} = r_{41}F_2 ,~~~~~\Delta a_{6}=r_{41}F_3 \end{align}\]
といった電界による屈折率変化が生じることになります。電界 \(F\) 印加時の楕円体の式は、\(\overline43m\) の結晶は電界のないときは等方性であることを考慮するとつぎのようになります。
\[\frac{x^2 +y^2 +z^2}{n_o^2}+\frac{2r_{41}F}{\sqrt{3}}\left (yz+xz+xy \right )=1\tag{10}\]
この楕円体について主軸変換を行うことにより、電界印加時の屈折率が求められるわけですが、ここでは付録に示した主軸変換をまともに行わずに \(\overline43m\) 結晶に特有な性質を用いて求めてみます。
電界印加方向<111>は3回回転軸で、この軸は主軸の一つのままです。他の2軸は<111>方向に垂直な面内にあります。<111>方向をz' 軸に選ぶと
\[z'=\frac{1}{\sqrt{3}}x+\frac{1}{\sqrt{3}}y+\frac{1}{\sqrt{3}}z\tag{11}\]
と表されます。さらに
\[\begin{align}x' &= \frac{1}{\sqrt{2}}y-\frac{1}{\sqrt{2}}z \\ y' &= -\frac{2}{\sqrt{6}}x+\frac{1}{\sqrt{6}}y+\frac{1}{\sqrt{6}}z\end{align}\tag{12}\]
となります。(11)、(12)式をx、y、zについて解き直すと
\[\begin{align}x &= -\frac{2}{\sqrt{6}}y'+\frac{1}{\sqrt{3}}z' \\ y &= \frac{1}{\sqrt{2}}x'+\frac{1}{\sqrt{6}}y'+\frac{1}{\sqrt{3}}z' \\ z &= -\frac{1}{\sqrt{2}}x'+\frac{1}{\sqrt{6}}y'+\frac{1}{\sqrt{3}}z'\end{align}\tag{13}\]
が得られます。この関係を(10)式に代入すれば、x'y'z'座標系での楕円体の方程式が得られます。計算が少しやっかいですが、結果を示すと
\[\left (\frac{1}{n_0^2}-\frac{r_{41}F}{\sqrt{3}}\right )\left (x'^2+y'^2\right )+\left (\frac{1}{n_0^2}+\frac{2r_{41}F}{\sqrt{3}}\right )z'^2=1\tag{14}\]
となります。電界 \(F\) により変化したx’、y’、z’方向の屈折率をそれぞれ \(n_{x'}\)、\(n_{y'}\)、\(n_{z'}\) とすると、(14)式から、左辺第1項の係数が \(1/n_{x'}^2 =1/n_{y'}^2\) に相当し、左辺第2項の係数が \(1/n_{z'}^2\) に相当します。このままでは電界 \(F\) に対する屈折率の変化がわかりにくいので、これらを \(F\) についてテーラー展開し、1次の項までとる近似を用いると、つぎの結果が得られます。
\[\begin{align}n_{x'} &= n_{y'}\simeq n_0 +\frac{n_0^3 r_{41}F}{2\sqrt{3}} \\ n_{z'} &\simeq n_0 -\frac{n_0^3 r_{41}F}{\sqrt{3}}\end{align}\tag{15}\]
この屈折率変化が実際にどの程度かを見積もってみましょう。GaAsを例にとって文献値を使って大雑把に計算してみます。\(r_{41}\) の値は波長1μm程度でおおよそ1×10-12m/V程度です。同じ波長での \(n_0\) は大体3.3くらいとされています。これより \(n_0^3 r_{41}\) の値は10-11m/Vのオーダーとなります。したがって \(F=10^6\) V/mの電界(厚さ1mmの結晶に1000Vの電圧をかける)をかけても屈折率の変化は10-5程度で、非常に僅かです。
例2.水素結合型結晶
大きなポッケルス効果をもつ結晶として水素結合型と呼ばれる一群の誘電体が知られています。代表的な物質はKDPと略称されることが多いリン酸二水素カリウム(KH2PO4)です。これも立方晶系である点では閃亜鉛鉱型と同類ですが、閃亜鉛鉱の \(\overline43m\) とは少し異なる \(\overline42m\) という対称性をもっています。KDP以外ではADP(リン酸二水素アンモニウム)もよく知られています。
\(\overline43m\) と \(\overline42m\) は4回回転軸をもつ点で共通ですが、異なるのは\(\overline42m\) は3回回転軸ではなく2回回転軸をもつ点です。2回回転軸は4回回転軸に垂直で互いに垂直な2つの軸です。4回回転軸をz軸にとると、二回回転軸はx軸、y軸にとることができます。
上記の\(\overline43m\)\の場合同様に考え、x軸の周りの180°回転から\(r_{12},r_{13},r_{22},r_{23},r_{32},r_{33},r_{42},r_{43},r_{51},r_{61}\) はすべて 0 となります。また、y軸の周りの180°回転から、\(r_{11},r_{21},r_{31},r_{53},r_{62}\) も 0 となります。さらにz軸周りの90°回転から\(r_{41}=r_{52}\neq 0\) 、\(r_{63}\neq 0\) であることがわかります。
したがって \(\overline42m\) の電気光学定数テンソルは
\[\pmatrix{0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr r_{41} & 0 & 0 \cr 0 & r_{41} & 0 \cr 0 & 0 & r_{63}}\]
となります。ここで電界 \(\boldsymbol{F}\) をz軸方向にかけた場合を考えます。すなわち \(\boldsymbol{F}=(0,0,F_z)\) とします。屈折率楕円体は
\[\frac{x^2 +y^2}{n_0^2}+\frac{z^2}{n_e^2}+2F_z r_{63}xy=1\tag{16}\]
となります。この場合はx、y軸を45°回転する変換を行えば、xyの項を省くことができるので、主軸変換の計算を行う必要はありません。新しい座標を \((x',y',z')\) とすれば
\[\begin{align}x &= x'\cos 45^{\circ}-y'\sin 45^{\circ}=\frac{\sqrt{2}}{2}(x'-y') \\ y &=x'\sin 45^{\circ} +y' \cos 45^{\circ}=\frac{\sqrt{2}}{2}(x+y) \\ z &= z'\end{align}\]
の関係があるので、(16)式は
\[\left ( \frac{1}{n_0^2}+r_{63}F_z \right )x'^2 +\left ( \frac{1}{n_0^2}-r_{63}F_z \right )y'^2 +\frac{z'^2}{n_e^2}=1\]
と変換されます。これより電界印加による屈折率を\(n_{x'}\)、\(n_{y'}\)、\(n_{z'}\) とすると、(15)式同様にして
\[\begin{align}n_{x'} &= n_0 -\frac{1}{2}r_{63}n_0^3 F_z \\ n_{y'} &= n_0 +\frac{1}{2}r_{63}n_0^3 F_z \end{align}\tag{17}\]
の関係が得られます。
例3.LiNbO3結晶
電気光学効果を利用した光変調器などに用いられる典型的な材料としては、強誘電体であるニオブ酸リチウム(LiNbO3)が古くからよく知られ、研究もされてきました。この結晶の構造は三方晶系の 3m であることが知られています。電気光学定数テンソルは上記の立方晶のように簡単には求められませんが、4つの独立要素をもち、8つの要素が 0 でない次のような形をもっていることが知られています。NbをTaに置き換えたタンタル酸リチウム(LiTaO3)も類似の特性をもつ結晶として知られています。
\[\pmatrix{0 & -r_{22} & r_{13} \cr 0 & r_{22} & r_{13} \cr 0 & 0 & r_{33} \cr 0 & r_{42} & 0 \cr r_{42} & 0 & 0 \cr -r_{22} & 0 & 0}\]
この結晶に \(\boldsymbol{F}=\left (F_x ,F_y ,F_z \right )\) の電界が印加された場合、屈折率楕円体は次式で表されます。
\[\begin{align} &\left (\frac{1}{n_0^2}-r_{22}F_y +r_{13}F_z \right )x^2 +\left (\frac{1}{n_0^2}+r_{22}F_y +r_{13}F_z \right )y^2 +\left (\frac{1}{n_0^2}+r_{33}F_z \right )z^2 \\ &- 2r_{22}F_x xy+2r_{51}F_y yz+2r_{51}F_z zx=1\end{align}\]
簡単な例として電界がz方向に印加された場合(\(F_x =F_y =0\))を考えます。この場合、屈折率楕円体は
\[\frac{x^2 +y^2 }{n_0^2 \left (1-\frac{1}{2}n_0^2 r_{13}F_z \right )^2}+\frac{z^2}{n_0^2 \left (1-\frac{1}{2}n_0^2 r_{33}F_z \right )^2}=1\]
となります。したがってxyz方向の屈折率 \(n_x\)、\(n_y\)、\(n_z\) の \(F_z\) 印加による変化は
\[\begin{align}n_x &=n_y \simeq n_0 -\frac{1}{2}n_0^3 r_{13}F_z \\ n_z &\simeq n_0 -\frac{1}{2}n_e^3 r_{33}F_z \end{align}\tag{18}\]
と表されます。
(2)2次の電気光学効果(カー効果)
2次の効果とは(3)式あるいは(4)式で右辺第3項による効果のことで、カー(Kerr)効果とも呼ばれています。この場合は電界の2乗による効果ですから、1次の効果のように方向が反転した場合、符号が変わるようなことがありません。このため、等方性の物質でも効果が生じます。一般に2次の効果は1次の効果より小さく、1次の効果があるとき、2次の効果は無視できる場合が普通です。このため等方性物質で2次の効果が顕著に観測されます。固体に限らず、液体誘電体でも観測されるのはこのためです。
1次の効果の場合と同様に、電界 \(\boldsymbol{F}=\left (F_x ,F_y ,F_z \right )\) が印加された場合、屈折率楕円体は(1)式で表されるものから(2)式で表されるものに変化するとします。ただし、2次の効果なので、(2)式の係数はそれぞれつぎのように表されます。
\[\begin{align}\left (\frac{1}{n^2 }\right )_1 &= \frac{1}{n_0^2}+s_{11}F_x^2 +s_{12}\left (F_y^2 +F_z^2\right ) \\ \left (\frac{1}{n^2 }\right )_2 &= \frac{1}{n_0^2}+s_{11}F_y^2 +s_{12}\left (F_z^2 +F_x^2\right ) \\ \left (\frac{1}{n^2 }\right )_3 &= \frac{1}{n_0^2}+s_{11}F_z^2 +s_{12}\left (F_x^2 +F_y^2\right ) \\ \left (\frac{1}{n^2 }\right )_4 &=s_{44}F_y F_z ,~~~~~~\left (\frac{1}{n^2 }\right )_5 =s_{44}F_z F_x ,~~~~~~\left (\frac{1}{n^2 }\right )_6 =s_{44}F_x F_y \end{align}\]
電界がz方向である場合(\(F_x =F_y =0\) は
\[\frac{1}{n_{x,y}^2}=\frac{1}{n_0^2}+s_{12}F_z^2\]
\[\frac{1}{n_z^2}=\frac{1}{n_0^2}+s_{11}F_z^2\]
となります。これより屈折率 \(n_x\)、\(n_y\)、\(n_z\) は近似的につぎのように表されます。
\[n_{x,y} \simeq n_0 -\frac{1}{2}n_0^3 s_{12}F_z^2\]
\[n_z \simeq n_0 -\frac{1}{2}n_0^3 s_{11}F_z^2\]
z方向に光を入射したとき、この方向での屈折率変化 \(\Delta n\) は
\[\Delta n =n_z -n_{x,y} =\frac{1}{2}n_0^3 \left (s_{11} -s_{12}\right )F_z^2 \]
であり、これによる波長 \(\lambda\) の光に生じる位相変化 \(\Gamma\) は、光路長を \(l\) とすると
\[\begin{align}\Gamma &= \frac{2\pi}{\lambda}n_0 \Delta n l\\ &= \frac{2\pi}{\lambda}\frac{n_0^2}{2}\left (s_{12}-s_{11}\right )l\left (\frac{V_z}{d}\right )^2 \tag{17}\end{align}\]
となります。この位相変化を考慮してカー効果の大きさの指標としてのカー定数 \(K\) をつぎのように定義しています。
\[K=\frac{n_0^3}{2\lambda}\left (s_{11}-s_{12}\right )\tag{19}\]
この \(K\) を用いると屈折率変化 \(\Delta n\) は
\[\Delta n=K\lambda F^2\tag{20}\]
と表されます。
このカー効果が観測される例として液体誘電体がしばしば挙げられます。例としてはニトロベンゼンなど有機物の液体があります。水(純水)でも観測されます。固体ではチタン酸バリウムやタンタル酸カリウムなどの結晶が挙げられます。これらはm3mの対称性をもち、一次の電気光学効果は生じません。
(1) この考え方を「現象論」と言います。固体の性質を明らかにするためにそれを構成する原子1個1個にまで遡り、互いに及ぼす相互作用を含めて計算する必要がある場合、それは現実的には困難です。しかし対象とする現象から得られる法則が比例関係かせいぜいそこからわずかに逸脱する程度と予測されるのであれば、初めから級数展開した関数を仮定して議論を進めても厳密な解析結果と大きな違いはないであろうという考えが現象論です。固体と電磁波(光)の相互作用ではこのような現象論的な取り扱いをする例が多くみられます。