科学・基礎／半導体物理学

３０．ブリルアンゾーン

　１次元の場合、格子の周期が \(a\) であれば、電子波の波数 \(k\) の範囲　　　\[-\frac{\pi }{a}\lt k \lt \frac{\pi }{a}\] を第１ブリルアンゾーンと呼ぶことは２６項で示しました。それでは３次元の場合はどうなるでしょうか。その前にまずは２次元で考えてみます。

　前項で示したようにブリルアンゾーンの境界ではブラッグ条件 　　　\[n\lambda = 2a\sin \theta\] が成り立ちます。第１ブリルアンゾーンでは、\(n=1\) とし、\(k=2\pi/\lambda\) と置き換えると 　　　\[k\sin \theta = \frac{\pi }{a}\] となります。この関係を２次元の図に描くと図３０－１のようになり、\(\theta\) が変化するとベクトル \(\mathbf{k}\) の終点の軌跡は \(x=\pi/a\) の直線になります。y 方向も同様に考えると、図３０－２の正方形で囲まれた範囲が２次元の第１ブリルアンゾーンとなります。この直線を画面に垂直な平面と考えれば、３次元のブリルアンゾーンになることが推測できます。

　ところで図３０－３のように２次元の碁盤の目に原子が並んでいると考えると、原子はなにも x 方向と y 方向にだけに周期をもって並んでいるわけではありません。例えば x、y 方向と 45°傾いた方向の直線（赤色の線）上にも並んでいます。ただしこの場合直線間の距離は \(a\) ではなく、\(a/\sqrt 2\) と短くなります。この面でのブラッグ反射の条件は 　　　\[k\sin \theta = \frac{\pi \sqrt{2}}{a}\] となります。この場合、\(\theta\) が変化するとベクトル \(\mathbf{k}\) の終点の軌跡は図３０－４の斜めの直線になります。この斜めの線で囲まれた領域で、さきの第１ブリルアンゾーンの外側に当たる領域が第２ブリルアンゾーンということになります。

　２次元の第１、第２ブリルアンゾーンを描いたのが図３０－５です。以上を３次元に拡張することはできそうですが、いろいろな原子の並び方がある実際の３次元結晶に対応させるやり方が以上ではまだはっきりしないと思います。

　原子が２次元空間に並んでいる場合をもう一度考えます。図３０－３に示すように原子が x､y 軸に垂直な直線上に碁盤の目のように並んでいて、この直線の間隔周期が \(a\) であるとします。これらの原子が並ぶ線に対応した逆格子ベクトルを定義にしたがって求めることができます。ｘ 軸に垂直な直線上にある原子に対応する逆格子ベクトルは、図３０－６に示す青色のベクトルで表され、x 軸方向に長さ \(2\pi/a\) のベクトルで代表されます。

　このベクトルが描かれている図３０－６は現実の空間（実空間と言います）を示してはいません。実空間が逆格子の定義に従って変換された空間のことを逆格子空間と呼びます。逆格子ベクトルをこの逆格子空間内に描いたのが図３０－６です。

　つぎにx軸、y軸に 45°斜め方向の直線（図３０－６に赤色で示す）について見ると、この直線上にも原子が規則的に並んでいます。線の間隔は上の場合より短くなって \(a/\sqrt{2}\) です。この線上に並ぶ原子の逆格子ベクトルは図３０－６に示すように斜め 45°方向に長さ \(2\pi\sqrt{2}/a\) の赤色のベクトルで表されます。

　原子の並ぶ等間隔の直線はいろいろとることができ、それぞれに対して逆格子ベクトルが定義できます。図３０－６に示した点は上記の２種類の逆格子ベクトルと向きが違うだけのベクトルの終点（逆格子点といいます）を示しています。

　この図３０－６の破線で囲んだ部分は２次元のブリルアンゾーンとよく似ていることがわかります。ブリルアンゾーンの境界は \(\pi/a\) を単位に表されていましたが、逆格子はその２倍の \(2\pi/a\) が単位になっています。

　２次元のブリルアンゾーンは電子の波のブラッグ反射から考えました。ですから \(\pi/a\) は波数 \(k\) の値です。一方、逆格子は結晶中の原子の並び方だけで決まりますから、\(2\pi/a\) の値は波数の値とは言えません。本来両者はなんの関係もなさそうですが、実際には上のように、よく符合することが分かります。

　図３０－６に示すように原点から一番近い逆格子点は４点ありますが、原点とこれらの点を直線で結び、その線分の垂直二等分線を４本引くと、この４本の直線で囲まれる範囲が第１ブリルアンゾーンとなります。また原点と原点から２番目に近い４点の逆格子点を結ぶ線の垂直二等分線を引くと、第２ブリルアンゾーンが得られます。以下、同様に第３、第４のブリルアンゾーンも求めることができます。

　結晶構造がわかれば逆格子点は求められますから、上記の方法によりブリルアンゾーンを容易に決められます。この方法をウィグナー・サイツ(Wigner-Seitz)の方法と呼びます。第10ブリルアンゾーンまで描いた複雑な図形を文献(1)に見ることができます。

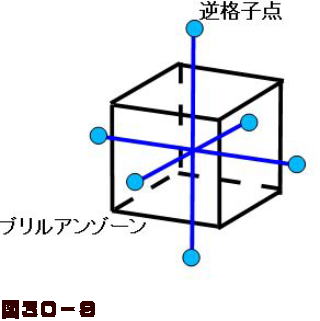
　以上は２次元でしたが、直線を平面に拡張して同じように考えれば３次元のブリルアンゾーンを求めることができます。もっとも簡単な例として図３０－７のような格子定数 \(a\) の単純立方格子を考えます。図３０－８（ａ）に示すように、この結晶の xyz 軸に垂直な面をそれぞれ \(\left(100\right)\)、\(\left(010\right)\)、\(\left(001\right )\) と表しますが、この面と平行で間隔が \(a\) の面上にも原子が並んでいます。これら一群の平面に対応する逆格子点の座標は \(\left(2\pi/a,0,0 \right)\)、\(\left ( 0,2\pi/a,0\right )\)、\(\left (0,0,2\pi/a\right)\) となります。原点に逆格子ベクトルの始点を置くと、終点がこれらの点になります。この他にこれらと原点に関して対称な３点もありますので、等価な逆格子点は全部で図３０－９に示すように６点があります。

　ウィグナー・サイツの方法によれば、各逆格子ベクトルの中点を通り、ベクトルと垂直に交わる平面で囲まれる立体、すなわち図３０－９に示す立方体が単純立方格子の第１ブリルアンゾーンということになります。

　２次元の場合と同様に３次元結晶の場合も原子が規則的に並ぶいろいろな面をとることができ、それらは等間隔で並びます。例えば図３０－８（ｂ）に示す \(\left( 110\right)\) 面は面間隔、周期は \(\sqrt{2a}/2\) です。この面は立方体を回転させると \(\left ( 101\right )\)、\(\left ( 011\right )\) 面など６通りの等価な面ができます。\(\left ( 110\right )\) 面の逆格子点の座標は (\(2\sqrt{2}\pi/a\), \(2\sqrt{2}\pi/a\),0) となります。そのためこの方向の第１ブリルアンゾーンの境界は原点からの距離が \(\sqrt{2}\pi/a\) となり、先程の距離とは異なる点が重要です。

　さらに図３０－８（ｃ）の \(\left ( 111\right )\) 面は面間隔、周期は \(\sqrt{3}a\) です。この面の逆格子点の座標は (\(2\sqrt{3}\pi/a\), \(2\sqrt{3}\pi/a\), \(2\sqrt{3}\pi/a\) ) となります。この方向の第１ブリルアンゾーンの境界は原点からの距離が \(\sqrt{3}\pi/a\) となり、上の２つと異なります。

　このように３次元の場合、結晶の面方向によってブリルアンゾーンの境界までの距離が異なるのが特徴です。ということは方向によって異なる波数のところでエネルギーギャップが生じることになります。

(1)植村泰忠、菊池誠著、「半導体の理論と応用（上）」、裳華房 第２章、２－１８図