科学・基礎／半導体デバイス物理

２０．量子井戸

　近年の発光ダイオードや半導体レーザではその発光層（活性層）に非常に薄い半導体層を用いるのが一般的になっています（発光ダイオードの９項、半導体レーザの３１項など）。この薄い層のことを量子井戸、複数積層したものを多重量子井戸と呼んでいます。「井戸(well)」というのは水が湧き出る深い穴のことですが、量子井戸の場合は電子をその波長より短い範囲に閉じ込めることができるポテンシャルエネルギーの窪みのことを言います。結晶成長技術の進歩で厚さ数ｎｍという極薄の結晶層が形成できるようになって実現したものです。

　上記の発光素子には化合物半導体が使われますが、この化合物半導体は一般に組成が異なるとバンドギャップエネルギーが異なります。バンドギャップエネルギーが異なる半導体を積層すると、電子はエネルギーの低い伝導帯をもつ半導体の部分に落ち込みやすいので、このエネルギーが低い部分が高い部分に囲まれていると、電子はエネルギーの低い部分（井戸）に閉じ込められることになります。

　このような狭い範囲に閉じ込められた電子の振る舞いは量子力学の典型的な対象です。量子井戸という言葉もこのことを示しています。ここでは量子井戸についての量子力学による解析について基礎的な部分を紹介します。まずは一次元のポテンシャル井戸について考えます。つまりポテンシャルエネルギー \(V\) が図２０－１のような形をしている場合（\(x\) 方向に幅 \(2a\) の井戸）を考えます。

　半導体物理学のセクションの１７項で取り上げているように、量子力学における基本方程式はシュレディンガー方程式です。この方程式に図のポテンシャルエネルギーを適用すれば量子井戸内の電子の振る舞いが解析できるはずです。

　１次元のシュレディンガー方程式の基本形は \[\frac{\mathrm{d}^{2} \psi}{\mathrm{d} x^{2}}=-\frac{2m}{\hbar^{2}}\left ( E-V \right )\psi \tag{1}\] です。ここで \(m\) は粒子、例えば電子の質量です。

　まずはじめに、ポテンシャル \(V\)が井戸の外側では無限に高い、 \[x \lt -a,~~a \lt x~~:~~V=\infty\] \[-a \leq x \leq a~~:~~V=0\] のような場合（破線で示す）を考えます。シュレディンガー方程式（１）は \[\frac{\mathrm{d}^{2}\psi}{\mathrm{d}x^{2}}=-\frac{2m}{\hbar^{2}}E\psi\tag{2}\] となります。この式をみると、関数 \(\psi\) の２階微分がもとの \(\psi\) に等しいような関数が解になりますから、少し強引かもしれませんが \[\psi\left (x\right )=A\sin \alpha x+B\cos \alpha x \tag{3}\] をシュレディンガー方程式（２）の一般解と考えてよいでしょう。ただし \[\alpha = \left ( \frac{2mE}{\hbar^{2}}\right )^{\frac{1}{2}}\tag{4}\] です。

　\(V=\infty \) の領域には粒子は入りこめませんから、 \[x=\pm a~~:~~\psi =0\] という境界条件が適用されます。すなわち \[A\sin \alpha a+B\cos \alpha a=0\] \[-A\sin \alpha a+B\cos \alpha a=0\] したがって \[A\sin \alpha a=0\] \[B\cos \alpha a=0\] です。\(A=B=0\) では \(\psi=0\) となってしまって意味がないので、それ以外のつぎの２通りの解が得られます。

\(A=0\) かつ \[\cos \alpha a=0\tag{5}\]

\(B=0\) かつ　 \[\sin \alpha a=0\tag{6}\]

　これが成り立つのは \[\alpha a=\frac{n\pi}{2}\] のときです。ただし（５）式の場合は \(n\) が奇数、（６）式の場合は \(n\) が偶数となります。これより解は

\(n\) が奇数のとき \[\psi \left ( x \right )=B\cos \frac{n\pi x}{2a}\] \(n\) が偶数のとき \[\psi \left ( x \right )=A\sin \frac{n\pi x}{2a}\] となります。\(A\) と \(B\) は規格化の条件 \[\int_{-a}^{a}\psi^{2}\left (x \right )\mathrm{d}x=1\] によって決めることができます。 \[\int \cos^{2}x\mathrm{d}x=\frac{1}{2}x+\frac{1}{2}\sin x\cos x\] \[\int \sin^{2}x\mathrm{d}x=\frac{1}{2}x-\frac{1}{2}\sin x\cos x\] という積分公式（積分定数省略）を使って \[A=B=\frac{1}{\sqrt{2a}}\] が得られるので、結局波動関数は

\(n\) が奇数のとき、 \[\psi \left ( x\right )=\frac{1}{\sqrt{2a}}\cos \frac{n\pi x}{2a}\tag{7}\] \(n\) が偶数のとき \[\psi \left ( x\right )=\frac{1}{\sqrt{2a}}\sin \frac{n\pi x}{2a}\tag{8}\] となります。

　またエネルギー固有値 \(E_{n}\) は \[E_{n}=\frac{\pi^{2}\hbar^{2}n^{2}}{8ma^{2}}\tag{9}\] となります。\(E_{n}\) は \(n^{2}\) に比例することがわかりますから、\(n=1,2,3,4\) に対応するエネルギーは図２０－２に示すようなイメージになります。井戸内の電子がとるエネルギーはこのような跳び跳びの値だけが許されることになります。井戸構造のない通常の伝導帯の電子のエネルギー分布はほぼ連続的であるのとは大きく異なります。このような量子井戸内のエネルギー準位を巧みに利用した例としては量子カスケードレーザ（半導体レーザの３７項）などが挙げられます。

　つぎに \(V\) が有限（無限大でない）の場合を考えます。（１）式の \(x \lt -a\)、\(x \gt a\) における一般解は \[\psi \left ( x\right )=C\exp \left ( -\beta x\right )+D\exp \left ( \beta x \right )\tag{10}\] で与えられます。ただし \[\beta =\left [ \frac{2m\left ( V-E \right )}{\hbar^{2}}\right ]^{\frac{1}{2}}\tag{11}\] です。ここで粒子が井戸内に閉じ込められる \(E \lt V\) の場合を考えます。すなわち \(\beta\) は実数です。

　境界条件としてまずは波動関数が遠方で発散しないことが必要ですから、\(x=\pm \infty\) において \(\psi =0\) が要求されます。このため、

\(x \lt -a\) において \[C=0\] \(a \lt x\) において \[D=0\] となります。

　さらに \(x= \pm a\) で \(\psi\) と \(\mathrm{d}\psi/\mathrm{d}x\) が連続であるという条件が必要です。これよりつぎの４つの条件が得られます。

\(x=a\) において \[A\sin \alpha a+B\cos \alpha a=C\exp \left ( -\beta a \right )\tag{12}\] \[\alpha A\cos \alpha a-\alpha B\sin \alpha a=-\beta C \exp \left ( -\beta a \right )\tag{13}\] \(x=-a\) において \[-A\sin \alpha a +B\cos \alpha a=D\exp \left ( -\beta a \right )\tag{14}\] \[\alpha A\cos \alpha a +\alpha B\sin \alpha a=\beta D \exp \left ( -\beta a \right )\tag{15}\] となります。この４式をつぎのように整理します。

（12）－（14）： \[2A\sin \alpha a=\left ( C-D \right )\exp \left ( -\beta a \right )\tag{16}\] （13）＋（15）： \[2\alpha A\cos \alpha a=-\beta \left ( C-D \right )\exp \left ( -\beta a \right )\tag{17}\] （12）＋（14）： \[2B\cos \alpha a=\left ( C+D \right )\exp \left (-\beta a \right )\tag{18}\] （15）－（13）： \[2\alpha B\sin \alpha a=\beta \left ( C+D \right )\exp \left ( -\beta a \right )\tag{19}\]

　ここで \(A=0\) かつ \(C-D=0\) でなければ、（17）式両辺を（16）式両辺によりそれぞれ割算して \[\alpha\cot\alpha a=-\beta\tag{20}\] また、\(B=0\) かつ \(C+D=0\) でなければ、同様に（19）式を（18）式により除して \[\alpha\tan\alpha a=\beta\tag{21}\] が得られます。（20）、（21）式は同時に成立できないので、 \(A=0\)、\(C=D\)　かつ \[\alpha \tan \alpha a=\beta\tag{22}\] また、 \(B=0\)、\(C=-D\)　かつ \[\alpha \cot \alpha a=-\beta\tag{23}\] となります。これが境界条件の式です。

　つぎに固有エネルギーを求めます。波動関数（３）と（10）について境界条件（22）、（23）が成り立っている条件でのエネルギーは解析的に求めることは困難です。ここではグラフを使った解法を紹介します。そのために少し数式的にテクニックが必要です。

　（22）式と（23）式の両辺に \(a\) をかけるとこの２式は \(\alpha a\) と \(\beta a\) の関数になることがわかります。そこで \(u=\alpha a\)、\(v=\beta a\) とおくと、(22)、（23）式は \[u\tan u=v\tag{24}\] \[u\cot u=-v\tag{25}\] と \(u\)、\(v\) の関数となります。

　また（４）式と（11）式で表される \(\alpha\) と \(\beta\) は、この２式を２乗して足すことによりエネルギー \(E\) を消去すると \[\alpha^{2}+\beta^{2}=\frac{2mV}{\hbar^{2}}\] という関係があることがわかります。この式の両辺に \(a^{2}\) をかけると \[u^{2}+v^{2}=\frac{2mVa^{2}}{\hbar^{2}}\tag{26}\] という関係が得られます。

（24）、（25）式と（26）式とがともに成り立つのが許される状態の条件です。そこで円の方程式である（26）式を示すグラフ（黒線）と（24）、（25）式のグラフ（赤線と青線）をそれぞれプロットしたのが図２０－３ですが、このグラフの交点が許されるエネルギー固有値となります。

　ここでは（26）式の円の半径を５としました。\(5 \gt \pi\) ですから、\(\tan \left ( x\right )\) が発散する \(\pi\) より円の半径が大きくなりますから、交点は図２０－３のように複数になります。\(\cot \left ( x\right )\) の場合も同様です。

　ここで（７）、（８）式の波動関数のイメージを \(n=1,2\) の場合について図示すると、図２０－４の上の図のようになります。単純な三角関数で、\(x= \pm a\) で \(\psi =0\) となります。

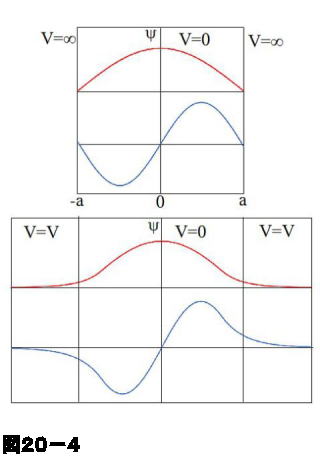
　\(V\) が有限な場合は、\(-a \lt x \lt a\) の範囲では（７）、（８）式と同じ関数に従いますが、この範囲の外側では上で議論した通り、指数関数となり、かつ境界条件によって \(x= \pm a\) で連続となります。そのイメージは図２０－４の下の図のようになります。つまり電子はポテンシャル障壁の内部にしみこむように存在できるようになることがわかります。