科学・基礎/半導体デバイス物理
14.ショットキー障壁の高さ金属-半導体接触の障壁はショットキーバリアダイオードとかMESFETなどに積極的に活用されますが、それ以外はむしろ障壁が小さく整流性のない電極(オーミック電極)の方が求められます。どちらの場合もショットキー障壁の高さの設定については金属電極の材料選択が重要になります。
前項までの議論をもとにすると、n型半導体に対しては仕事関数の小さい金属を選ぶ方が電子に対する障壁が低くなり、p型半導体に対しては逆に仕事関数の大きな金属を選ぶと正孔に対する障壁が小さくなりますから、オーミック電極を形成する場合、基本的にはこのような指針で電極金属が選択されます。
しかしこのような指針で選んだ金属が実用的にはいろいろな問題があって使えなかったり、必ずしも予想通り良好なオーミック電極が得られない場合も多く、実際には金属を半導体表面に着けた後で熱処理をして半導体表面で金属と半導体を合金化するなどの工夫がなされる場合も多いです。
具体的な例に少し触れておきます。たとえばS.M.Sze著の"Physics of Semiconductor Devices"にはデータが載っています。まず金属の仕事関数ですが、もっとも大きいのは白金(Pt)で5.3Vくらいの値です。もっとも小さいのはセシウム(Cs)、フランシウム(Fr)といったところで、1.8Vくらいの値になっています。
一般によく使われる金属で仕事関数が大きいのは金(Au)やパラジウム(Pd)が4.8V程度の値です。小さい方ではマグネシウム(Mg)が3.6V、インジウム(In)が3.8Vといったところです。その他、よく使われるアルミニウム(Al)、チタン(Ti)、クロム(Cr)、ニッケル(Ni)、銅(Cu)、銀(Ag)、スズ(Sn)といった金属は4~4.5Vの値をもっています。
既に説明しているように、電子に対するショットキー障壁の高さは上記の金属の仕事関数 \(\psi_{m}\) と半導体の電子親和力 \(\chi\) の差です。シリコンの電子親和力は約4.0Vとされていますが、Auの仕事関数が上記のように約4.8Vですから、ショットキー障壁の高さは0.8Vと予想されます。上記の本にはAu/Siの組み合わせのショットキー障壁の高さの測定値として0.79V前後の値であることが示されており、予想とよく合っていることがわかります。
しかしいつもこのように予想とよく合うわけではないようです。それは半導体の表面に表面準位ができてここに電子が捕らえられることによると考えられています。物質の表面は内部と違って特殊な状態にあるので、なかなか一筋縄ではいかないのです。
さて以上とは別の原因でショットキー障壁は上記の \(\psi_{m}-\chi\) より低くなることが知られています。これを最後に紹介しておきます。
図14-1に示すように真空中に置いた金属板に電荷、例えば電子が接近すると、金属には電子とは反対の正の電荷が誘起されます。これによって電子には金属板の方向に引きつける力がはたらきます。これは金属板の表面の位置に対して対称な位置に電子と同じ電荷量の正電荷を置いたときにはたらく力 \(F\) と等価になります。これを鏡に映る像に見立てて「鏡像効果」と呼んでいます。これはクーロン力ですから、電子と金属板の距離を \(x\) として \[F=-\frac{e^{2}}{4\pi \varepsilon _{0}\left ( 2x \right )^{2}}\] と書けます。電子のもつポテンシャルエネルギー \(\phi\) は \[e\phi =-\int_{\infty }^{x}Fdx=-\frac{e^{2}}{16\pi \varepsilon _{0}x}\] となります。なお、図の電気力線は正確なものではなく、あくまでイメージです。真空の側が半導体であっても同様な力がはたらくと考えられます。
電界 \(E\) が印加されると、図14-2に示すように電子のポテンシャルエネルギーは \[e\phi =-\frac{e^{2}}{16\pi \varepsilon _{0}x}-eEx\] のように変化します。これを \(x\) で微分し、それが 0 となる点 \(x_{m}\) は \[x_{m}=\left ( \frac{e}{16\pi \varepsilon _{0}E}\right )^{1/2}\] と求められますが、ここで \(\phi\) は最大となります。この点での \(\phi \left(x_{m}\right )\) は \[e\phi \left ( x_{m} \right )=-e\left ( \frac{eE}{4\pi \varepsilon _{0}} \right )^{1/2}\] となり、\(E=0\) のとき、\(x \rightarrow \infty\) で \(\phi=0\) にとっていますから、これより上式の分だけ障壁が下がることになります。低下分を改めて \(\Delta\phi\) とすると \[e\Delta \phi =\phi \left ( \infty \right )-\phi \left ( x_{m} \right )=e\left ( \frac{eE}{4\pi \varepsilon _{0}} \right )^{1/2}\] となります。
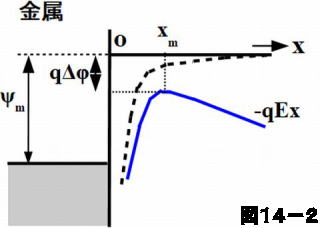
この外部電界に依存した仕事関数の低下をショットキー効果と呼んでいます。ショットキー障壁が生じることをショットキー効果と呼ぶかのように混同しやすいので(そんなことはない?)、注意が必要です。
以上は真空中の金属表面の話でしたが、金属-半導体接触でも同様に考えられ、ショットキー障壁は \(\psi_{m}-\chi\) よりも低くなります。数値的には0.1V程度ですから、それほど影響が大きいわけではありません。