結晶の話

科学・基礎／結晶の話

８．結晶構造の分類

（１）二次元格子 　前項の図に示した通り、二次元格子の特徴は基本単位ベクトル \(\boldsymbol{a}\)、\(\boldsymbol{b}\) の大きさ \(|\boldsymbol{a}| =a\)、 \(|\boldsymbol{b}| =b\) となす角 \(\gamma\) によって表されます。

　この３つの要素で分類すると図８－１に示す５種類の基本格子ベクトルに集約されます。

　

図８－１

平面斜方格子 \(a\ne b ,\gamma \ne 90^\circ\) 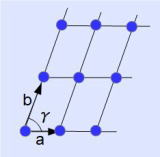長方格子 \(a\ne b ,\gamma = 90^\circ\)

面心長方格子 \(a\ne b ,\gamma = 90^\circ\) 正方格子 \(a = b ,\gamma = 90^\circ\)

六方格子 \(a = b ,\gamma = 60^\circ\)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　ここで例えば、面心長方格子があるのに面心正方格子がありません。これは図８－２に示すように、黒線で示す面心正方格子は必ず赤線で示す正方格子で代表されるからです。

　また \(|\boldsymbol{a}|=|\boldsymbol{b}|\) で、\(\gamma\) が \(90^\circ\)でも \(60^\circ\)でもない場合がないのは、面心長方格子で代表されるからです。これはつぎのように証明できます。図８－３に示すように、ベクトル \(\boldsymbol{a}+\boldsymbol{b}\) と \(\boldsymbol{a}-\boldsymbol{b}\) を考えると、\(|\boldsymbol{a}|=|\boldsymbol{b}|\) であれば、そのなす角は \(\gamma\) によらず直角になります。これはベクトル \(\boldsymbol{a}+\boldsymbol{b}\) と\(\boldsymbol{a}-\boldsymbol{b}\) の内積が \(|\boldsymbol{a}|=|\boldsymbol{b}|\) であれば 0 になることから明らかです。

　その他あらゆる二次元格子は上記５種類ですべて表されることが確認できます。

（２）三次元格子 　三次元格子の場合は基本単位ベクトル \(\boldsymbol{a}\)、\(\boldsymbol{b}\)、\(\boldsymbol{c}\)の大きさ（長さ）\(a\)、\(b\)、\(c\) の大小関係となす角 \(\alpha\)、\(\beta\)、\(\gamma\)が90°または120°に等しいか否かなどによって表されます。この結果、下記７種類の基本格子ベクトル系に集約され、これらがさらに頂点にしか原子が存在しない単純格子だけでなく、結晶面上に原子が存在する底心格子，体心格子、面心格子を含む場合があり、図８－４に示すように、すべてで計14種類に分類されます。これを分類者の名前を冠してブラベー格子（Bravais Lattice）と呼びます。

１．三斜晶系(Triclinic) 、２．単斜晶系（Monoclinic）、３．斜方晶系（Orthorhombic）、４．正方晶系（Tetragonal)、５．六方晶系（Hexagonal）、三方晶系（Trigonal）（菱面体晶系、Rhombohedral）、７．立方晶系（Cubic）

図８－４

結晶形単純底心体心面心対称性

三斜晶系 \[a\ne b\ne c\]\[\alpha\ne\beta\ne\gamma\] \[\bar{1}\]

単斜晶系 \[a\ne b\ne c\]\[\alpha =\gamma =90^\circ\]\[\beta\ne 90^\circ\] \[\frac{2}{m}\]

斜方晶系 \[a\ne b\ne c\]\[\alpha=\beta=\gamma=90^\circ\] \[\frac{2}{m}\frac{2}{m}\frac{2}{m}\]

正方晶系 \[a=b\ne c\]\[\alpha=\beta=\gamma=90^\circ\] \[\frac{4}{m}\frac{2}{m}\frac{2}{m}\]

六方晶系 \[a=b\ne c\]\[\alpha=\beta=90^\circ\]\[\gamma=120^\circ\] \[\frac{6}{m}\frac{2}{m}\frac{2}{m}\]

三方晶形（菱面体晶系） \[a=b=c\]\[\alpha=\beta=\gamma\]\[\lt 120^\circ,\]\[\ne 90^\circ\] \[\bar{3}\frac{2}{m}\]

立方晶系 \[a=b=c\]\[\alpha=\beta=\gamma=90^\circ\] \[\frac{4}{m}\bar{3}\frac{2}{m}\]

**図８－１**
平面斜方格子	\(a\ne b ,\gamma \ne 90^\circ\)	長方格子	\(a\ne b ,\gamma = 90^\circ\)
面心長方格子	\(a\ne b ,\gamma = 90^\circ\)	正方格子	\(a = b ,\gamma = 90^\circ\)
六方格子	\(a = b ,\gamma = 60^\circ\)

　

結晶形		単純	底心	体心	面心	対称性
三斜晶系	\[a\ne b\ne c\]\[\alpha\ne\beta\ne\gamma\]					\[\bar{1}\]
単斜晶系	\[a\ne b\ne c\]\[\alpha =\gamma =90^\circ\]\[\beta\ne 90^\circ\]					\[\frac{2}{m}\]
斜方晶系	\[a\ne b\ne c\]\[\alpha=\beta=\gamma=90^\circ\]					\[\frac{2}{m}\frac{2}{m}\frac{2}{m}\]
正方晶系	\[a=b\ne c\]\[\alpha=\beta=\gamma=90^\circ\]					\[\frac{4}{m}\frac{2}{m}\frac{2}{m}\]
六方晶系	\[a=b\ne c\]\[\alpha=\beta=90^\circ\]\[\gamma=120^\circ\]					\[\frac{6}{m}\frac{2}{m}\frac{2}{m}\]
三方晶形（菱面体晶系）	\[a=b=c\]\[\alpha=\beta=\gamma\]\[\lt 120^\circ,\]\[\ne 90^\circ\]					\[\bar{3}\frac{2}{m}\]
立方晶系	\[a=b=c\]\[\alpha=\beta=\gamma=90^\circ\]					\[\frac{4}{m}\bar{3}\frac{2}{m}\]